Homework 7 (due 6/4)
CSC 202

We finished Section 8.2 and covered chapter 9. Next week we will come back to parts of Section 8.3 and see additional material not in the notes yet.

See the butterfinger prove Euler's theorem.

And a clip from the Simpson's about Lisa and Tremeaux's algorithm: Homer lost in the maze. The maze page has a good description of Tremaux's algorithm (there are several incomplete/imprecise versions on the web, so beware).

For fractals, check out the wikipedia page; it's a good starting point (it has an animation of the full Koch snowflake).

Remember that we won't meet next week (5/28), and that the final will be on 6/11 (two hours, open book, not cumulative).

Submission: you can submit the homework to me either by hardcopy in class or email it to me.

1. [Topological Sort, 10pt] In class I mentioned another algorithm to topologically sort a graph; recall that for a directed graph the out-degree of a vertex is the number of edges leaving the vertex (as opposed to entering the vertex). Given a dag G, that is a directed acyclic graph, proceed as follows: repeatedly (and as long as you can) pick a vertex of out-degree 0, remove it and all its outgoing edges from G. The vertices are a topological sort in the order you remove them.

Why does a dag always contain a vertex of out-degree 0? Hint: what would a graph look like in which every vertex has out-degree at least 1?

2. [Euler Tours, 10pt] An Euler tour in a directed graph is a directed walk in the graph (that is a walk respecting the directions of the edges) that traverses every directed edge exactly once. State (don't prove) a version of Euler's theorem for directed graphs, i.e. when does a directed graph have an Euler tour? Include examples of directed graphs that have an Euler tour, and ones that do not, and show how your criterion applies in those cases.

3. [Bipartite Graphs, 20pt]

a) [5pt] Prove that all trees are bipartite.

b) [15pt] For each of the following two parties, decide whether everybody can be seated at at most two tables so that no two people that hate each other have to sit at the same table. Either show a seating arrangement (with hate relationships drawn so that it is clear that they only occur between tables) or give the reason that such a seating arrangement is not possible.

3. [Figurative Numbers, 25pt]

a) [10pt] What is the sum of the first n odd numbers? Give both a geometric (pebbles) and an algebraic (equations) argument (as we did in class).

b) [15pt] Show that H(n) = n + 4 T(n-1), where H(n) is the nth hexagonal number (see notes, page 158). Conclude that H(n) = n(2n-1). Hint: Remember what we did with pentagons and triangular numbers. A proof could be a drawing of how to do this for H(4) or H(5), say, which shows that your method generalizes to H(n).

4. [Fractals, 20pt] What is the area of the full Koch snowflake (see wikipedia animation). To construct the full snowflake start with an equilateral triangle of area 1 (you don't need to know the side-lengths to solve the problem). In each step subdivide every side of your current snowflake into three pieces and erect a new equilateral triangle on the middle third of the side.

  1. [5pt] What is the length of the full Koch snowflake?
  2. [15pt] What is the area of the full Koch snowflake?

5. [Extra Credit] The magician asks you to think of a number between 1 and 16. He then shows you the following four cards:

1 3 5
7 9 11
13 15  
2 3 6
7 10 11
14 15  
4 5 6
7 12 13
14 15  
8 9 10
11 12 13
14 15  

 You tell the magician on which of the cards your number appears. The magician can immediately tell you what your number is on.

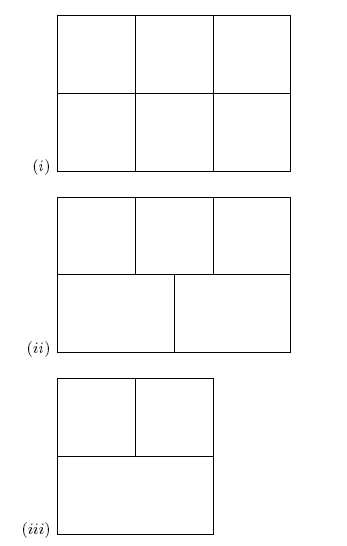
6. [Extra Credit] For each of the following pictures, (i)-(iii) try drawing a curve through the figures that crosses each line of the figure exactly once. Hint: this might not be possible in all cases, in which case you want to argue why it is not possible.

3. [Extra Credit] If you find any typos and mistakes in the lecture notes, please let me know.

Marcus Schaefer
Last updated: May 22nd, 2007