CSC 241 Lab 9
Submission: Submit the python or text file that contains all your answers to the submission folder for this lab by the end of the lab. To simplify Drew's (our tutor) work, please include your name and the number of the lab at the top of the file (if you're submitting a Python file, use comments: start the line with a #).
Grading: see the grading criteria for lab assignments.
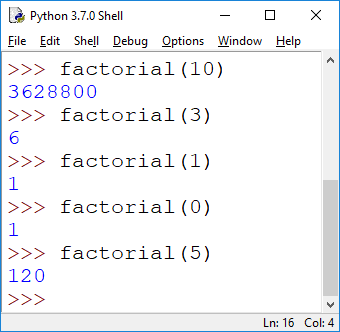
1. (While Loop) Implement the factorial function factorial(n) which calculates 1*2* ... * n. We've done this before, here the difference is: don't use the built-in factorial, and don't use a for loop. Work with a while loop.
2. (While Loop - Statistics) We want to find out how many throws of a die it takes to get a 6. To do this, write two functions: die() and stats(n):
a) A call of the die() function repeatedly rolls a die until it comes out 6. The function counts how often you have to roll the die before you get the 6 and returns that count. Here are some test-runs:
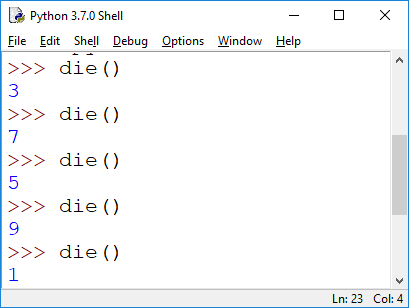
So in the last call to die() the very first roll gave a 6. In the call before that, it took 9 times. Hint: use the randrange(a,b) function in the random module to simulate a die-roll (remember that a is inclusive, and b is exclusive), and a while loop to keep going until you have a 6.
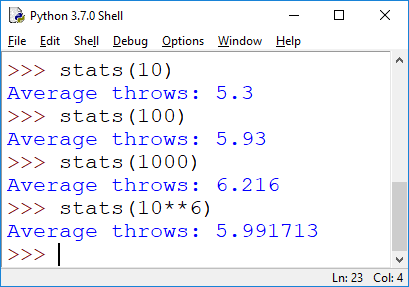
b) Write a function stats(n) that calls the die() function n times, and records each outcome. At the end, it then reports the average value of all outcomes. We'd expect it to 6 rolls on average to get a six, so the larger n, the closer we should get to 6. This is borne out by the following test-runs (the last one took a couple of seconds to complete).
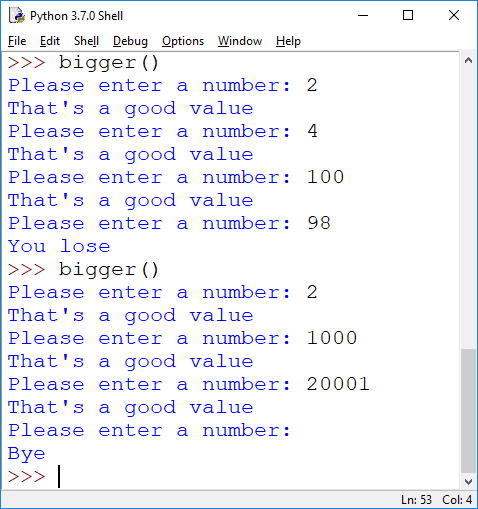
3. (While Loop) Here's a somewhat silly game: you alternate naming numbers that always have to be strictly larger than the previous one. Write a function bigger() that supports playing this game. The game starts with 0; if anybody enters a number lower than the previously highest number the game ends with the player losing. Entering nothing simply ends the game.
Marcus Schaefer
Last updated:May 22nd, 2019.