Homework 5 (due 5/10)
CSC 401

We have been talking about different loop programming patterns.In particular we saw nested loops (Section 5.2) and two-dimensional lists and how to process them using nested loops (Section 5.3). After the midterm we talked about the while loop (Section 5.4, 5.5, 5.6). Next week, we will see one or two more while loop examples, and then continue with dictionaries (6.1), tuples and sets (6.2) and string encoding (6.3). 

I mentioned that some programmers consider break statements harmful; this goes back to a famous essay by Edgar Diskstra called Go to statement considered harmful.If you google the title, you'll also find more recent discussion on what programmers think about the issue these days.

1. (Reading Assignment) Read Sections 5.3-5.6 of the textbook. If you want to read ahead, read 6.1 and 6.2.

2. (Figures, 10pt) We saw some simple nested loops creating figures, including a square and a triangle; in this problem we want to use nested loops to create two more triangles. For both of these problems do not use tricks like string multiplication to create asterisks, really print each asterisk separately using nested loops.

a) Write a function triangle(n) which creates n rows of asterisks, with n asterisks in the first row, down to 1 asterisk in the last row. Here is a screenshot for n = 4. The asterisks should be right-aligned. 

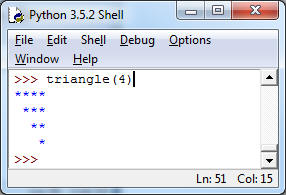
Hint: there are two solutions (as we saw in class): two separate inner loops, one for spaces, one for asterisks, or, more flexibly, one inner loop with an if to distinguish whether you need a space or an asterisk. 

b) Write a function rect(n,m) which creates the boundary of an nxm rectangle, that is an nxm (empty) box with asterisks in the first and last columns and rows. 

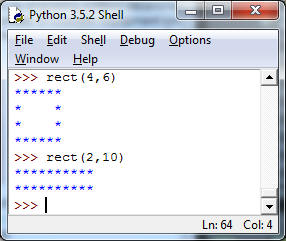
Hint: Here it'll be better to have the inner loop use an if.

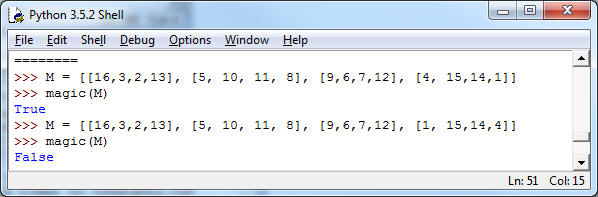
3. (Magic Square, 10pt) In class we saw a program magic(M) that tested some of the conditions for a square matrix M to be a magic square, namely it tested that all the rows have the same sum. Extend this program so it also checks that all the column-sums are the same. The sample run below (with Duerer's magic square) is successful; for the second M, I switched two of the numbers in the last row, so the row sums remain the same (so our initial program would have failed to detect this change), but the column sums are now no longer correct. The first column has column sum 16+5+9+1 = 31, whereas all row- and column-sums in this example should be 34.

4. (While Loop, 10pt) Write a program upper() that keeps prompting the user for words until they simply hit return. At that point, the program should return the number of upper-case words entered by the user. See test-runs below.

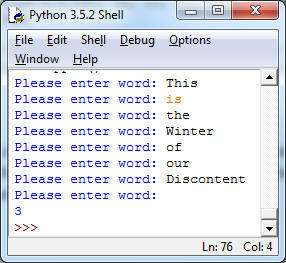
Hint: Either infinite loop or loop-and-a-half are fine for this. For practice you may want to do _both_ versions.

5. (More While Loops, 10pt) You've been keeping track of your planned bank account transactions, and it doesn't look so good, e.g. you had the following transactions in the list lst. Positive values are incoming money, negative values are money spent.

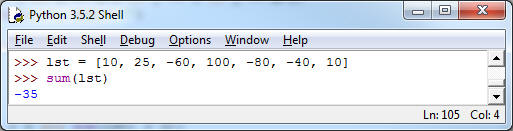
As you see that left you $35 short. Your strategy to deal with this is to remove the largest amount spent to improve the situation. In this case removing the $80 you were planning to spend bring you to a positive budget. In general, you may have to remove more than one of the negative numbers, but you'll always remove them in order of value, that is largest negative transactions get eliminated first, until you reach a positive budget. Write a program improve(lst) which implements that strategy and prints the remaining transactions as well as the overall resulting budget. If this is not possible (if you're only spending money), the program should warn you about that.

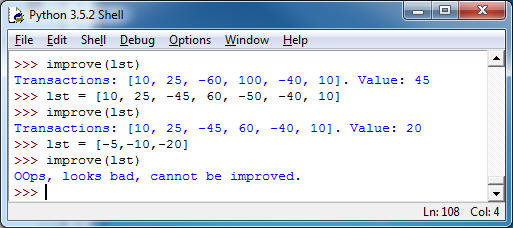
Hint: this is a pretty short, simple program, don't overcomplicate it. Do it by hand on one or two examples, then in the shell, and then implement. The min or max function may be useful.

6. (Extra Credit, 5pt) Extend the magic square code so that it also checks that the two diagonals have the same sum as the rows and columns.