We talked about brute force, approximation and parameterization in class.

Submission: you can submit the homework to me either by hardcopy in class or email it to me.

1. [Largest Independent Set, 20pt] We want to improve the running time of the algorithm finding a largest independent set using some observations.

1. Suppose all vertices in a graph have degree at most 1. Show that the largest independent set in the graph has size |V| - |E|. Hint: what does such a graph look like.
2. Use the observation in (a) to improve the algorithm we saw in class; find the recurrence relation for your modified algorithm.
3. On top of b, preprocess the graph by first dealing with vertices of degree at least 3; find the recurrence of the algorithm after adding this preprocessing step.

For both b. and c. include your pseudocode.

2. [Wigderson coloring, 10pt] Wigderson's coloring algorithm finds a 3sqrt(n) coloring of a 3-colorable graph. Improve the algorithm so it finds a sqrt(8n) coloring of a 3-colorable graph. Hint: modify the degree cut-off.

3. [Coloring planar graphs, 20pt] The four-color theorem tells us that every planar graph, that is a graph that can be drawn in the plane without edges intersecting, can be colored using at most 4 colors. In this exercise we'll see an algorithm that colors planar graphs using at most 6 colors.

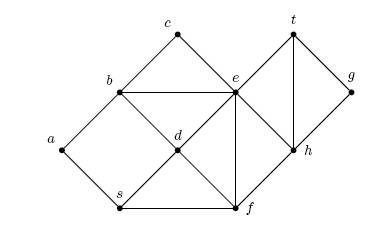
1. [10pt] Euler's formula states that n + f = 2 + m for a planar graph, where n = |V|, m = |E| and f is the number of faces (regions) of the graph, counting the outer face. E.g., consider the graph in the following picture; it has n = 10, m = 17, f = 9, so n + f = 19 = 2 + m. Using Euler's formula show that a  planar graph always has a vertex of degree at most 5. (Hint: assume, for a contradiction, that every vertex has degree at least 6.)

2. [10pt] Write pseudocode for a polynomial time algorithm that colors a planar graph using at most 6 colors.
3. [Extra Credit] How can you make the algorithm run in time O(|V| + |E|)?

4. [TSP, 20pt] Do Exercise 35.2-3 on page 1033 of the book.

5. [Extra Credit] Given an n x n matrix of zeros and ones, we can try to compress it by representing it as the union of at most k rectangles of ones. For example, the matrix

ooooooooooooo
ooooo111ooooo
oo111111111oo
oo111111111oo
ooooo111ooooo
ooooo111ooooo
oo111111111oo
oo111111111oo
ooooo111ooooo
ooooooooooooo