Homework 6 (due 11/5)
CSC 243


We completed talking about recursion, and have been talking about objects (Chapter 8). We will see some more examples of classes and then apply them to parse HTML pages.

Other topics we talked about:

Submission: The homework is due by midnight (I will not accept late homeworks). You can submit your homework through d2l into the drop-box for this homework.

Please prepare your homework as a single file containing all answers (e.g. doc, docx, or pdf, not a zip file). When submitting programs, include the programs, together with screenshots of test-runs of your program (make sure screenshots are sized so the text is legible; resize and/or crop the images). For an example, see hwexample.docx. How to take screenshots? Check out screenshots for MAC, Windows, Linux. Unless I ask for it specifically, you do not have to submit separate files with program code or executables. If multiple files are necessary, please do not zip them up, just submit them separately.

1. (Reading Assignment) Read Sections 10.3, and 8.1-8.4. I skipped sorting & search (a core CS topic you will see repeatedely in your programming career), but it won't hurt to check it out while thinking about recursion: see Section 10.4 for that. The towers of Hanoi (see above) are the case study for chapter 10. Another topic I skipped is how Python actually implement objects using namespaces; see Section 7 on namespaces if you want to find out more.

2. (HTML, 5pt) Next week, we will start working with HTML. So we do not have to spend a lot of time reviewing HTML, please read Section 11.1 of the book. There is no deliverable for this problem other than your updated mind in class next time.

For the following problems on recursion, you do have to use recursion. Do not use global variables and do not add arguments to  your functions.

2. (Collatz sequence, 10pt). Remember the Collatz sequence? It starts with a number. If that number is even, the next number is n//2, if it's odd, the next number is 3*n+1, and so on, until you  hit 1. E.g. starting with 10, you get 10,5,16,8,4,2,1. Write a recursive function collatz(n) which returns the list of all numbers in the Collatz sequence starting with n. No loops allowed.

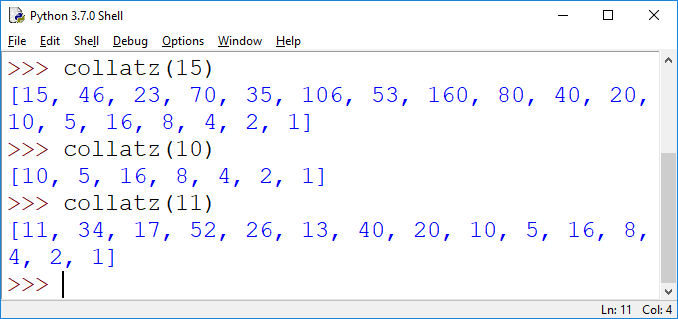
Hint: In a first step, you may always want to divide by 2. Then distinguish the two recursive cases.

3. (Traversal, 15pt) Two problems on finding files with certain properties in your folder structure using recursion. You are not allowed to use os.walk (or similar functions that simulate the recursive traversal for you).

a) [8pt] Write a program changed(path, k) that lists all files within path (and below it) which have changed (or are new) in the last k days. See below for two test-runs.

Note: Start with the traverse() function, and, in a first step, print the names (full paths) of all files. Then print the names together with how old they are. The function time() in the time module gives you the current time, compare that to the timestamp of the file (research the os.path module to find out which function to use for that).

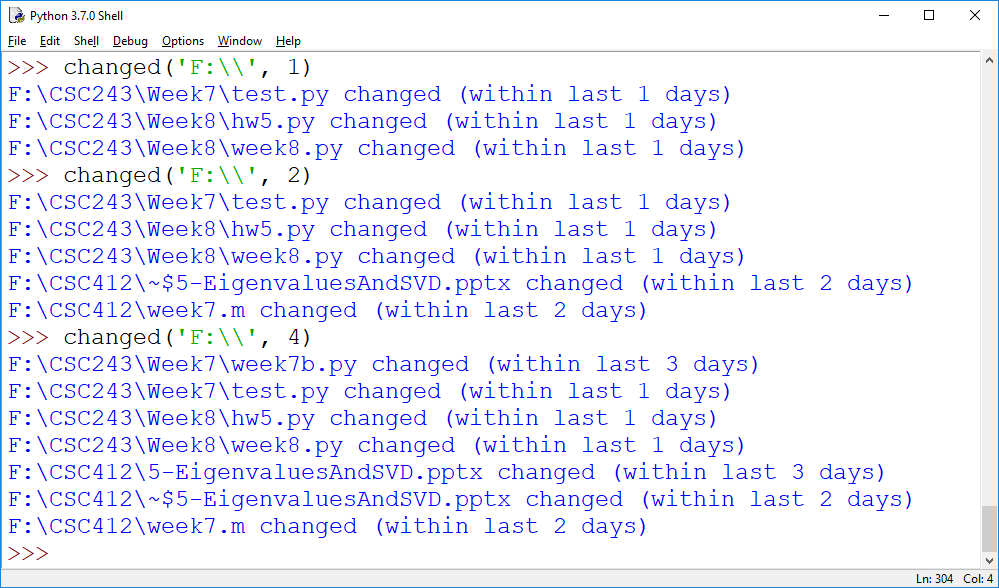
b) [7pt] Write a recursive function oldest(path) which returns the name and the age (in seconds) of the oldest file in path or below. Hint: Start by just returning the age (in seconds) of the oldest file (that's like a max computaiton). Then modify the returns so they return pairs of values, age and name.

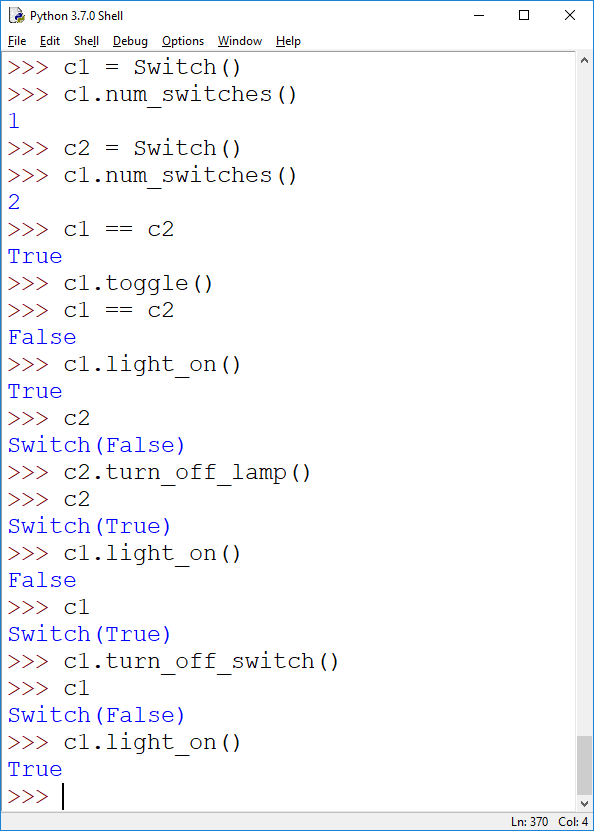
4. (Classes and Objects, 10pt) In class we implemented a Switch class (see the week8.py file on d2l). For this problem  you want to extend this class to support the following methods:

See below for test-runs.

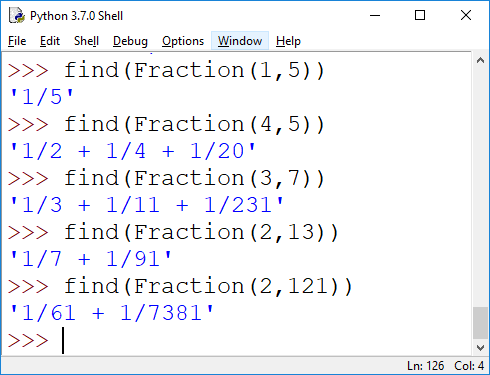
5. (Extra Credit, 10pt) You want to write a fraction a/b as a sum of fractions of the form 1/n, with distinct n. For example, 2/7 = 1/4 + 1/28. Implement a function find(f) which takes a fraction f (work with the built-in fractions module; it is called fractions) and returns a way to get f by summing up fractions of the form 1/n for distinct n. The way you look for these fractions should be greedy: if f is > 1/n, you include 1/n in your sum, and move on to the next n. For example,. take f = 2/7. That's not bigger than 1/1, 1/2, or 1/3. But it is bigger than 1/4. So we start with 2/7 = 1/4 + ... . This leaves us with 2/7- 1/4 = 1/28. We'll try n = 5 through 28, when we realize we are done, since 2/7 = 1/4 + 1/28. You can implement your solution recursively or iteratively. You do need to work with the fraction module, since the precision issues will become serious even for fractions f = a/b with small values of a and b. See some test-runs below. The code runs very fast in general, but there are inputs (e.g. 5/121) that will blow up your code, since some of the 1/n are astronomically far out.

Marcus Schaefer
Last updated: October 30th, 2019.