Homework
3 (due 4/22)
CSC 355
We have continued (and will continue) talking about SQL. This week's material corresponds to what the book covers in Sections 6.1, 6.2, and parts of 6.3 (6.3.6-6.3.8). Next week we'll cover Sections 6.3 and 6.4. After that we'll go back to Chapter 3 in the book for relational design.
Handing it in: Submit to the d2l dropbox. Use some standard format for your homework (Word or pdf, for example), and make sure to include your name and assignment number. Include screenshots for code and testruns.
1. (Reading Assignment) Read Sections 6.1-6.3 of the textbook (Ullman, Widom, A First Course in Database Systems).
2. (SQL, 6pt) On the last homework we added mentor information to the student table. We'll need this set-up for the current problem (my solution is on d2l if you want to use that). Make sure you assign mentors to several (but not all) of the students.
a) [2pt] Write a query which lists all students (SID, Lastname, Firstname) who have not been assigned a mentor.
b) [4pt] Our university has a rule that student mentors must be more senior than their mentees (i.e. must have started before). Write a query which lists all mentees (SID, Lastname) which have been assigned a mentor violating this rule. Hint: how many students are involved in this query?
As always, submit screenshots of both queries and output.
3. (SQL, 14pt) You have relation Orders(OrderID, CustomerID, NumberOfItems, ItemsTotal), Customer(CID, Name, State), StateTax(State, SalesTaxRate).
a) [4pt] Create SQL-DDL to create these tables (with foreign keys: CustomerID -> CID) and fill them with a small number of records. E.g. in State you could have ('Illinois', 6.25) and ('Michigan', 6) (do not include all US states).
b) [6pt] Write a query that lists all orders (by OrderID) and the expected price the customer has to pay. Calculate the expected price according to the following rules
-
The product cost of all items in the order together is ItemsTotal.
-
To this you need to add shipping costs; shipping costs are calculated as follows: each item by itself costs $0.99 in shipping. Items are bundled in shipments containing (up to) 4 items. Each shipment is $3.99. So two items incur a cost of $5.97 = 2*$0.99 + $3.99, and 5 items $12.93 = 5*$0.99 + 2*$3.99.)
-
Tax is calculated based on ItemsTotal. Everybody pays a basic sales tax of 4%. We also collect tax based on the customer's state's tax-rate (as recorded in StateTax) . So an Illinois customer pays an additional 6.25% on ItemsTotal (for a total of 10.25% in sales tax) and a Michigan customer 6% (a total of 10%).
c) [4pt] Improve the query to deal with the following situation: Sometimes our order records are incomplete (i.e. contain null values). If we don't have ItemsTotal, the query should not get an expected price for the order (i.e. it should be null). If NumberOfItems is missing, we assume it is 1. If there's a null entry for a state's sales tax in the table we assume it is 0. (Hint: Recall the coalesce function). Hand in your solution of c) separately from the solution to b).
As always, submit screenshots of both queries and output.
4. (3-valued logic, 10pt) Not all 2-valued truths are 3-valued truths. E.g. in 2-valued logic "A or not(A)" can always be replaced with "TRUE", but that's not the case in 3-valued logic (in which "A or not (A)" could be unknown, namely when A is unknown). In 2-valued logic there is a law (known as DeMorgan's law) which states that "not(A and B)" is equivalent to "not(A) or not(B)" for all truth-values of A and B. Intuitively, both are ways of expressing that not both A and B are true. We can prove the equivalence using a truth table in which we "plot" the truth values of "not(A or B)" compared to "not(A) and not(B)" for all combinations of A and B to verify that they are equal:
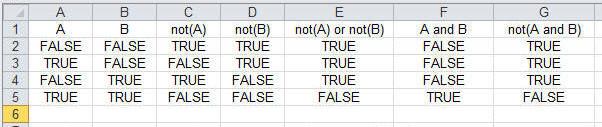
This is a useful law to have, and it could help us simplify some database queries ("not(A and B)" has one less negation than "not(A) or not(B)"), but is this law still true for 3-valued logic? Build a truth-table like the one above for all 9 possible combinations of truth-values of A and B, and calculate expressions "not(A)", "not(B)", "not(A) or not(B)", "A and B" and "not(A and B)" to check whether this law still holds for 3-valued logic. State explicitly whether DeMorgan's law holds for 3-valued logic or not.
5. (University SQL, 10pt) Write SQL for the following problems on the university database. Run each query. Submit screenshots of both query and output. Note: Do not use SQL features (e.g. GROUP BY) that we haven't seen in class.
-
List courses (CourseName, CID) and all students (SID, Lastname, Firstname) who enrolled in those courses. Courses should get listed even if nobody enrolled in them. On the other hand, you do not want to list students who haven't enrolled in a course.
-
List IDs of students who enrolled in Fall of 2013, but not in winter of 2013. Hint: yes, you just need to list IDs, and that's a bit of a hint. Think in terms of sets. Drawing a Venn diagram may help.
6. (Extra Credit, 10pt) Remember Date's example from class (last slide of the Basic SQL presentation). Date argues that queries can "produce results that are correct according to the three-valued logic but not correct in the real world". Some people would argue that the problem is with the query that Date writes:

Help Date write a correct query, i.e. a query that lists all pairs (SNO,PNO) "where either the supplied and part cities are different or the part city isn't Paris (or both)", even if there are null values in the city fields. Test-run it on a couple of examples to make sure it really works correctly. E.g. in Date's sample database
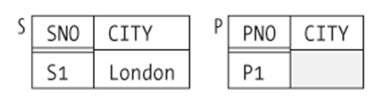
(S1,P1) should get listed (since City is either London, in which case it's different from Paris, or different from London, so supplier and part city are different and it should get listed). But the query should also still work if S.City contains null values (or, of course, other cities than London). Hint: there are four possible cases to consider depending on whether S.City and/or P.City are null. Analyze the four cases and figur out which of the cases cause the query above to fail (e.g. if both S.city and P.city are known, the query works just fine). Then add conditions to deal with that case/those cases. Briefly explain your reasoning for each case.
Marcus Schaefer
Last updated: April 16th, 2014.