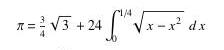Homework
7 (due 3/11)
CSC 431
This week we finished chapter 6 (6.5.3), covered parts of chapter 7 (7.1, 7.3.1, 7.3.2, parts of 7.3.4/7.3.5) and chapter 8 (8.1, 8.3). Next week we will cover some of the remaining topics in chapter 8 and go on to chapter 9. Also, next week I will hand out the take-home final (due one week later).
During class we saw some of Heath's simulations:
and we discussed some of my solutions to homework 6:
Bernoulli and the accuracy
problem.
Submission: you can submit the homework by hardcopy in class or by sending it to me as an email.
Note: for all of the problems on this homework you can use the computer, but still explain your steps.
1. [Horner's Scheme, 5pt] Rewrite f(x) 5x^4 - 10x^3 + 5x^2 - x + 7 using Horner's scheme and evaluate f(3) using Horner's scheme.
2. [Interpolation, 20pt] You have observed the following data:
| t | y = f(t) |
| -1 | 10 |
| 0 | 4 |
| 1 | 6 |
| 2 | 2 |
- Using polynomial interpolation (Vandermonde matrix), find an interpolant in the monomoial basis.
- Using Lagrange interpolation, find an interpolant in the Lagrange basis.
- How many additions/multiplications are needed to evaluate each of the two interpolants (assuming that you pre-compute divisors in the Lagrange interpolant and evaluate the polynomial interpolant using Horner's scheme)?
3. [Integration, 25pt] Newton derived the following formula to compute pi:
- Use Midpoint, trapezoid and Simpson's quadrature rules to approximate the integral and find an approximation to pi. Compute errors and compare.
- Using Gaussian quadrature with two and three points to approximate the integral and obtain an approximation to pi. We derived the locations of two points for the interval [-1,1]. See Gaussian quadrature for the locations of three points and how to change the interval from [-1,1] to [0,1/4]. Again, compute errors and compare (to the methods in a as well).
- Review composite quadrature rules (Example 8.6 of the book) and approximate the integral using composite midpoint and trapezoid rules by breaking the interval into n subintervals. Try various values of n. Again compute errors; at what value of n, roughly, are the composite rules comparable to Gaussian quadrature with three points?
- (Extra Credit) Derive the composite Simpson's rule for arbitrary n and apply it to approximate pi using the above formula. How does its accuracy compare to the composite midpoint and trapezoid rules?
Marcus Schaefer
Last updated: March 5th, 2010.