Homework
7 (due 5/26)
CSC 543
We covered more material on computational geometry, in particular we saw algorithms for interval overlap, rectangle intersection, point location, trapezoidation and triangulation, line segment intersection and area computation. The material is from the textbook and de Berg, van Kreveld, Overmars, Schwarzkopf, Computational Geometry, Springer, 2000. (Chapters 2, 3, 6). We also made a short excursion into the art gallery theorem. O'Rourke's book on the subject is now available online. There are also more specialized books on visibility algorithms. Next week we'll finish computational geometry and talk about chapter 6 of the textbook on indexing.
Submission: you can submit the homework by hardcopy in class or by sending it to me as an email.
1. [Convex Hull, 25pt] We saw a convex hull algorithm that computes the convex hull of n points in time O(n log n) and in general that's the best we can do. However, in application your point-set might have more structure. E.g. you might have to compute the convex hull of a simple polygon given by its boundary: p0, p1, ... pn. Show that in this case you can determine the points on the convex hull in time O(n). A high-level (precise) sketch or your algorithm will be sufficient. You should also argue that your algorithm takes linear time.
2. {Point Location, 25pt] Suppose we are given a convex polygon (by a listing of the points along its boundary). Using preprocessing time O(n log n) and storage O(n) show that we can tell whether any point lies inside or outside the polygon in time O(log n). Hint: the randomized point location algorithm we saw in class will solve the problem, however, in this special case (of a convex polygon), there is a much simpler algorithm based on the original idea of splitting the polygon up into slabs, which we discarded for general polygons since it used too much space. Does your algorithm generalize beyond convex polygons to a larger class?
3. [Extra Credit] Implement the formula for calculating the area of a polygon. Assuming the points of the polygon are pi = (xi, yi) in counterclockwise order, the area is:
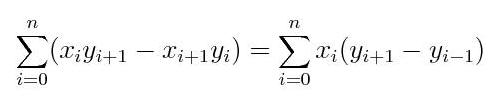
In these formulas, xn+1, yn+1 denote x0, y0 (this simplifies writing the formula). The two formulas are equivalent, so you can use either one, but the second one should be faster (since it only involves one multiplication rather than two). Given large data sets can you determine a performance difference between using the two formulas?
Marcus Schaefer
Last updated: May 21st, 2009.